GASES

Q.01: Select the most suitable answers from the given ones in each question:    

(i) Pressure remaining constant at which temperature the volume of a gas will become twice of what it is at 0^oC:

(a) 546^oC

(b) 200^oC

(c) 546 K

(d) 273 K

Ans: (c) 546 K

EXPLANATION: When a gas is present at 0^oC or 273 K, and its temperature is increased by 1^oC, its volume will increase by 1/273 of its original volume V_o at 0^oC i.e., its new volume will be V_o + V_o/273. In this way, if temperature is increased from 0^oC to 273^oC, the volume of the gas will become double.

(ii) Number of molecules in one dm³ of water is close to:

(a) 6.02/22.4× 10²³

(b) 12.04/22.4× 10²³

(c) 18/22.4× 10²³

(d) 55.6 × 6.02 × 10²³

Ans: (d) 55.6 × 6.02 × 10²³

EXPLANATION: 1 dm³ of water is equal to 1 kg of water because density of water is 1. One kg water contains 55.6 moles (Formula: n=m/M ➣1000/18=55.6). We know 1 mole of a compound contains 6.02 ✕ 10²³ molecules, so 55.6 moles of water contain 55.6 ✕ 6.02 ✕ 10²³ molecules of water.

(iii) Which of the followings, will have the same number of molecules at STP?

(a) 280 cm³ of CO₂ and 280 cm³ of N₂O

(b) 11.2 dm³ of O₂ and 32 g of O₂

(c) 44 g of CO₂ and 11.2 dm³ of CO

(d) 28 g of N₂ and 5.6 dm³ of oxygen

Ans: (a) 280 cm³ of CO₂ and 280 cm³ of N₂O

EXPLANATION: 280 cm³ of CO₂ and 280 cm³ of N₂O contain equal number of molecules because at STP, same volumes of different gases contain same number of moles as well as molecules (Avogadro’s Law). Since, both gases have same volumes, so their number of molecules are also the same.

(iv) If absolute temperature of a gas is doubled and the pressure is reduced to one half, the volume of the gas will be:                            

(a) Remain unchanged

(b) Increase four times

(c) Reduced to 1/4

(d) Be doubled

Ans: (b) Increase four times

EXPLANATION: If absolute temperature of gas is doubled, its volume will become double because volume is directly proportional to absolute temperature (Charles’ Law). When pressure on the same gas is reduced to one half, its volume will double again (Boyle’s Law). Thus, the net result will be four times increase in volume of the gas.

(v) How should the conditions be changed to prevent the volume of a given gas form expanding when its mass is increased?

(a) Temperature is lowered & pressure is increased.

(b) Temperature is increased & pressure is lowered.

(c) Temperature and pressure both are lowered.

(d) Temperature and pressure both are increased.

Ans: (a) Temperature is lowered & pressure is increased.

EXPLANATION: When mass of a gas is increased, its volume tends to be increased. If we want to prevent it from expanding, we will have to decrease its temperature and increase pressure on it, because lowering the temperature will decrease the motion of gas molecules and the molecules will come closer. Similarly, by increasing pressure, the molecules of gas come closer and the gas is finally compressed.

(vi) The molar volume of CO₂ is maximum at:

(a) STP

(b) 127^oC and 1 atm

(c) 0^oC and 2 atm

(d) 273^oC and 2 atm

Ans: (b) 127^oC and 1 atm

EXPLANATION: The volume of a gas is directly proportional to temperature and inversely proportional to pressure, so it will be maximum at high temperature and low pressure. When we calculate the volume of one mole of CO₂ under different conditions of temperature and pressure as given in the options above, by using general gas equation (PV=nRT), we come to know that it will be maximum at 127^oC temperature and 1 atm pressure.

(vii) The order of the rate of diffusion of gasses NH₃, SO₂, Cl₂, and CO₂ is:

(a) NH₃>SO₂>Cl₂>CO₂

(b) NH₃>CO₂>SO₂>Cl₂

(c) Cl₂>SO₂>CO₂>NH₃           

(d) NH₃>CO₂>Cl₂>SO₂

Ans: (b) NH₃>CO₂>SO₂>Cl₂

EXPLANATION: The rate of diffusion of a gas is inversely proportional the the square root of the its density or molar mass (Graham’s Law of Diffusion). Keeping in mind the molar masses of these gases, we conclude that their crates of diffusion will be in order of NH₃>CO₂>SO₂>Cl₂.

(viii) Equal masses of CH₄ and oxygen are mixed in an empty container at 25^oC. The fraction of total pressure exerted by oxygen is:       

(a) 1/3

(b) 8/9

(c) 1/9

(d) 16/17

Ans: (a) 1/3

EXPLANATION: The pressure exerted by a gas in a mixture of gases is directly proportional to the number of moles or molecules of that gas. The greater the mole fraction of a gas in a mixture, the greater will be its partial pressure and vice versa. The molar mass of oxygen (32 g mole^-1) is twice the molar mass of methane (16 g mole^-1). When equal masses of these two gases are taken, the mole fraction of oxygen will be half to that of methane. So, if total pressure is 3 atm, 2/3 of it will be exerted by methane while 1/3 will be exerted by oxygen.

(ix) Gases deviate from ideal behavior at high pressure. Which of the followings is correct for non-ideality?

(a) At high pressure, the gas molecules move in one direction only.

(b) At high pressure, the collisions between the gas molecules are increased manifold.

(c) At high pressure, the volume of the gas becomes insignificant.

(d) At high pressure, the intermolecular attractions become significant.

Ans: (d) At high pressure, the intermolecular attractions become significant.

EXPLANATION: At high pressure the gas molecules close to each other, their actual volume does not remain negligible as compared to the total volume of the vessel, and also they start attracting each other. So, the free volume available to gas molecules as well as the pressure exerted by them, do not match the values as predicted by ideal gas equation. The gas is now said to be deviating from ideality.

(x) The deviation of gas form ideal behavior is maximum at:

(a) –10^oC and 5.0 atm

(b) –10^oC and 2.0 atm

(c) 100^oC and 2.0 atm

(d) 0^oC and 2.0 atm

Ans: (a) –10^oC and 5.0 atm

EXPLANATION: Gases deviate from ideal behaviour at low temperature and high pressure because under these conditions, the gas molecules come close to each other. Their mutual distances are reduced so the actual volume of gas molecules does not remain negligible as compared to total volume of the vessel. Forces of attraction between gas molecules also start operating at lower distances, so real pressure becomes less than that predicted by ideal gas equation. Keeping in mind all these facts and putting the above values in van der Waal’s equation, the gas seem to deviate most from ideality at –10^oC temperature and 5.0 atm pressure.

(xi) A real gas obeying van der Waals equation will resemble ideal gas if:

(a) Both “a” and “b” are large

(b) Both “a” and “b” are small

(c) “a” is small and “b” is large

(d) “a” is large and “b” is small

Ans: (a) Both “a” and “b” are large

EXPLANATION: ‘a’ is called the attraction co-efficient. Lower is the value of attraction co-efficient of a gas, smaller will be the attraction between gas molecules, and less will be the deviation from ideal behaviour, and vice versa. ‘b’ is called excluded volume which is four times the actual volume of the gas molecules. The lower is the value ‘b’, greater will be the volume available for the free movement of gas molecules, and as a result less will the deviation from ideality. So, for a gas to resemble an idea gas, its ‘a’ and ‘b’ values must be small.

Q.02: Fill in the blanks.

(i) The product PV has the S.I. unit of ________.

(atm dm³)

(ii) Eight gram of each O₂ and H₂ at 27^oC will have the K.E. in the ratio of _________.

(1:16)

(iii) Smell of cooking gas during leakage from a gas cylinder is due to the property of ________ of gases.

(effusion)

(iv) Equal ________ of the ideal gases at the same temperature and pressure contain ________ number of molecules.

(volumes/equal)

(v) The temperature above which a substance exists only as a gas is called _________.

(critical temperature)

Q.03: Indicate true or false as the case may be.

(i) Kinetic energy of molecules of gas is zero at 0^oC.

(False)

Correct: Kinetic energy of molecules of gas is zero at 0 K.

(ii) A gas in a closed cylinder will exert much higher pressure at the bottom due to gravity than at the top. 

(False)

  Cor

Correct: Gas molecules exert equal pressure on all sides in a closed container because gravity does not affect the motion of gas molecules..

(ii) Real gases show ideal gas behavior at low pressure and high temperature.  

(True)

(iv) Liquefaction of gases involves decrease in intermolecular spaces.

(True)

(v) An ideal gas on expansion will show Joul-Thomson effect.

(False)

Correct: A highly compressed gas on sudden expansion from a small hole or jet produces cooling called Joule-Thomson effect.

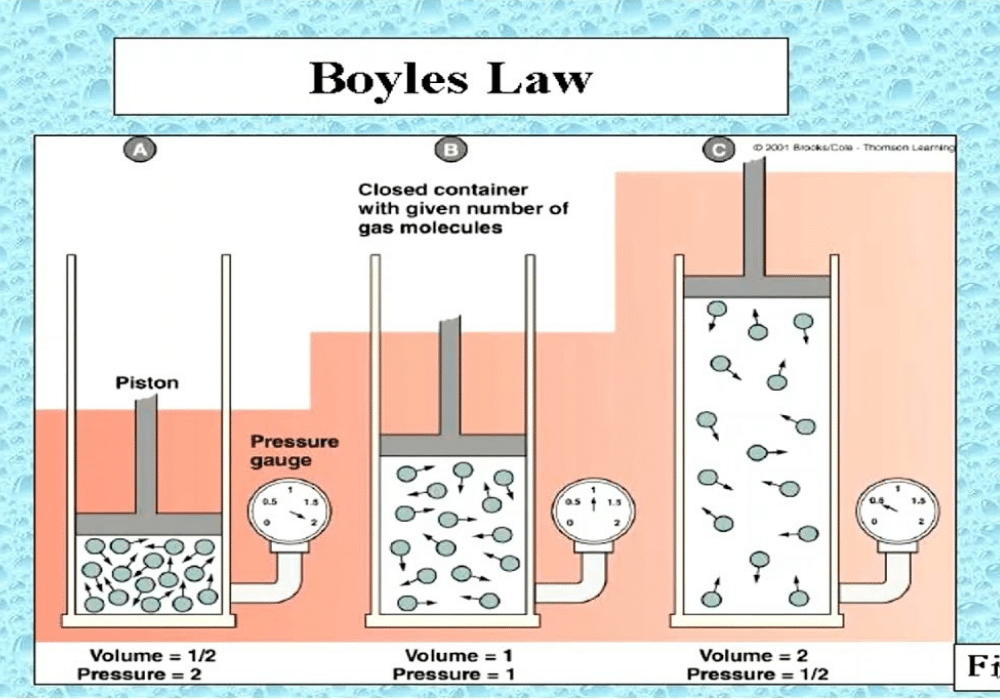
Q.4(a) What is Boyle’s law of gases? Give its experimental verification.

Ans: Boyle’s law is stated as follows: “The volume of a given mass of a gas at constant temperature is inversely proportional to the pressure applied to the gas.”

So, V∝1/P (when the temperature and number of moles are constant)

or V=k/p

PV = k (when T & n are constant) ___________ (1)

‘k’ is proportionality constant. The value of k is different for different amounts of the same gas.

According to the equation (1), Boyle’s law can also be defined as: “The product of pressure and volume of a fixed amount of a gas at constant temperature is a constant quantity.”

So, P₁V₁ = k and P₂V₂ = k

Hence, P₁V₁ = P₂V₂

Experimental Verification of Boyle’s Law:

Let us take a gas in a cylinder having a moveable piston. The cylinder is also attached with a manometer to read the pressure of the gas directly. Let the initial volume of gas is 1 dm³ and its pressure is 2 atmosphere when the piston has one weight on it. When the piston is pressed twice with the help of two equal weights, the pressure becomes four atmosphere. Similarly, when the piston is loaded with a mass three times greater, then the pressure becomes six atmosphere. The initial volume of the gas at two atmosphere is 1 dm³. It is reduced to 1/2 dm³ and then 1/3 dm³ with increase of weights, respectively.

(b) What are isotherms? What happens to the positions of isotherms when they are plotted at higher temperature for a particular gas?

(c) Why do we get a straight line when pressure exerted on a gas are plotted against inverse of volume? This straight line changes its position in the graph by varying the temperature. Justify it.

(d) How will you explain that the value of constant k in the equation PV=K depend upon

(i) The temperature of gas

(ii) The quantity of gas

Ans: In Boyle’s law, the value of proportionality constant ‘k’ depends upon temperature and quantity of gas. This is because ‘k’ is actually the product of pressure and volume of the gas. At constant temperature and quantity of gas, an increase in pressure will decrease the volume, keeping PV constant. But, when T and n are also increased along with pressure, the volume will not decrease as previous. It will have a greater value depending upon temperature and the quantity of gases added. So, the value of constant ‘k’ also changes accordingly.

Q.05: What is the Charles’s law? Which scale of the temperature is used to verify that V/T=K (pressure and number of moles are constant)

Ans: Charles’ law is a quantitative relationship between temperature and volume of a gas and was given by French scientist J. Charles in 1787. According to this law: “The volume of the given mass of a gas is directly
proportional to the absolute temperature when the pressure is kept constant.” i.e.,

V ∝ T (P & n are constant)

V = kT
V/T=k

Absolute or Kelvin scale of temperature is used to verify The Charles’ equation. i.e., V/T=k

(b) A sample of carbon monoxide gas occupies 150.0 ml at 25.0^oC. It is then cooled at constant pressure until it occupies 100.0 ml. What is the new temperature?       

Solution:

Data:

V₁ = 150 ml                           

V₂ = 100 ml

T₁ = 25^oC + 273  288 K      

T₂ = ?

Formula Applied:  

V₁/T₁ = V₂/T₂

T₂ = V₂T₁/V₁

T₂ = 100ml ✕ 288 K / 150 ml = 198.6 K

Ans: T₂ = 198.67 K or –74.33^oC.

(c) Do you think that the volume of any quantity of a gas becomes zero at -273.16^oC. Is it not against the law of conservation of mass? How do you deduce the idea of absolute zero from this information?

Ans: According to the definition of absolute zero, at –273.16^oC, the volume of every gas becomes equal to zero. But, practically, it is not possible because zero volume means no volume. It means gas will no longer exist at that temperature. This is against the law of conservation of mass which says that matter can neither be created nor destroyed, though it may be changed from one form into another. Actually, no gas can achieve this temperature, because all the gases become liquid and solids before attaining this temperature.

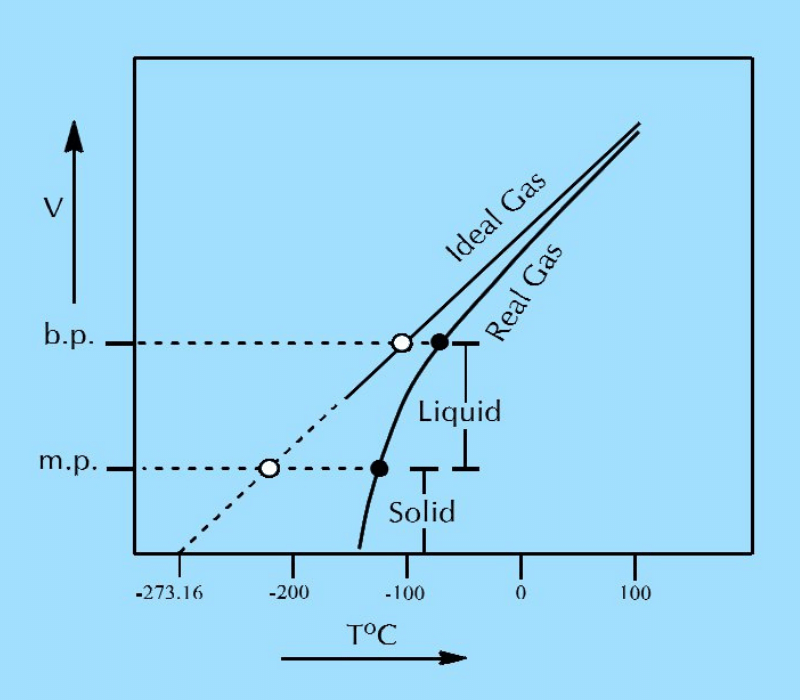
Q.06(a): What is Calvin scale of temperature? Plot a graph for one mole of a real gas to prove that a gas becomes liquid, early that -273.16^oC.

Ans:

Absolute or Kelvin Scale: This is a scale of temperature at which the melting point of ice at 1 atmospheric pressure is 273K, and the boiling point of water is 373K or more precisely 373.16K.
Temperature on Kelvin scale = Temperature °C + 273.16

Graph showing that one mole of a real gas changes into a liquid and then solid before achieving absolute zero temperature.

(b) Throw some light on the factor 1/273 in Charles’ law.

According to quantitative definition of Charles’s law, if a gas is kept at constant pressure at 0^oC. Then for every one degree rise or fall of temperature, the volume of the gas will increase or decrease by   of its original volume at 0^oC. In this way, volume of a gas, at any temperature ’t’, can be calculated with the help of this factor. i.e.,

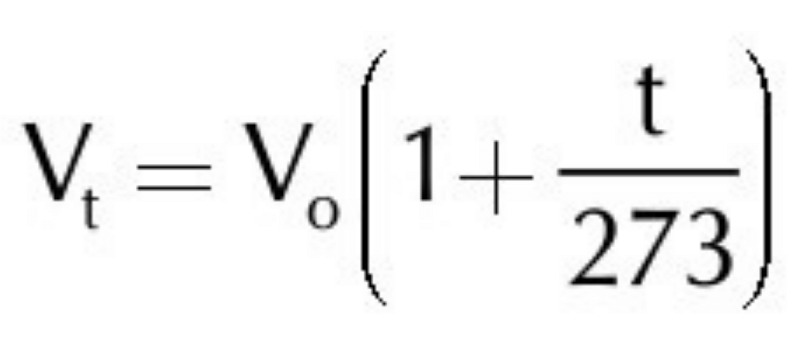
According to this equation, if the temperature of a gas is increased from 0^oC to 273^oC, the volume of the gas will become double. And, if the temperature is decreased from 0^oC to –273^oC, the volume of the gas will become zero.

Q.07(a): What is the general gas equation? Derive it In various forms.

General Gas Equation: All gas laws can be combined to form general gas equation as:

According to Boyle’s law, V ∝ 1/P (When ‘n’ and ‘T’ are held constant)

According to Charles’s law, V ∝ T (When ‘n’ and ‘P’ are held constant)

According to Avogadro’s law, V ∝ n (When ‘P’ and ‘T’ are held constant)

When none of the variables are kept constant, the above three equations can be combined as:

V ∝ nT/P

V = constant nT/P

V = R nT/P

PV = nRT

This equation is called general gas equation or ideal gas equation. ‘R’ is general gas constant or universal gas constant. This equation shows that if we have any quantity of an ideal gas, the product of pressure and volume is equal to the product of number of moles, general gas constant and absolute temperature.

(b) Can we determine the molecular mass of an unknown gas if we know the pressure, temperature and volume along with the mass of that gas?

Ans: Yes, we can determine the molecular mass of an unknown gas if we know the pressure, temperature and volume along with the mass of that gas, by applying the following modified form of general gas equation:

PV = nRT

Or PV = m/M ✕ RT

Or M = m/PV ✕ RT

(c) How do you justify from general gas equation that increase in temperature or decrease of pressure decreases the density of the gas?

Ans: According to general gas equation:

PV = nRT

Or PV = m/M ✕ RT

Or PM = m/V ✕ RT

Or PM = dRT (∵ m/V=d)

Or d=PM/RT

This relation shows that density of gas is inversely proportional to temperature and inversely proportional to pressure. So, if temperature is increased, density of the gas will decrease and vice versa. Similarly, if pressure on the gas is decreased, density will also decrease and vice versa.

(d) Why do we feel comfortable in expressing the densities of gases in the units of g dm^-3 rather than gcm^-3, a unit which is used to express the densities of liquids and solids?

Ans: The densities of gases are so small that expressing them in normal units of g cm^-3 make calculations difficult. So, it is more convenient to express them in g dm^-3. While, the densities of liquids and solids are high enough to be expressed in normal units of g cm^-3.

Q.08(a): Derive the units for gas R in the general gas equation:

(a) When the pressure in atmosphere and volume in dm³.

Ans: According to Avogadro’s law, the volume of one mole of a gas at STP is 22.414 dm³. Putting these values of P, T, V & n in general gas equation, the value of R at STP can be calculated:

PV = nRT   or R = PV/RT

(b) When pressure is in Nm^-2 and volume in m³.

Ans: The SI unit of pressure is Nm^-2 and that of volume is m³. Applying SI units of P, T & V in the formula R = PV/ nT , the value of R can be calculated.

(c) When energy is expressed in ergs.

Ans: The value of R in Joules mol^-1K^-1:

R = 8.314J mol^-1K^-1

We know, 1J = 1 ✕ 10^-7 ergs

Or 1 J = 10000000 ergs

So, the value of R when energy is taken in ergs is:

R = 8.314 ✕ 10⁷ ergs mol^-1K^-1

Q.09(a): What is Avogadro’s law of gases?

Avogadro’s Law: Avogadro’s law states that: “Equal volumes of all the ideal gases at same temperature and pressure contain equal number of molecules.” For example,

22.414 dm³ of H₂ at STP = 1 mole of H₂ contain = 6.02 × 10²³ molecules of H₂

22.414 dm³ of CH₄ at STP = 1 mole of CH₄ contain = 6.02 × 10²³ molecules of CH₄

(b) Do you think 1 mole of H₂ and 1 mole of NH₃ at 0^oC and 1 atm pressure have Avogadro’s number of molecules?

No, 0^oC is such a low temperature. Under 1 atm pressure, 1 mole of H₂, being very small non-polar molecules, may exist as independent molecules, so contain Avogadro’s number (6.02 × 10²³) of molecules, but 1 mole of NH₃, being highly polar molecules with strong hydrogen bonding, doesn’t exist as independent molecules but in the form of irregular groups. So, 1 mole of NH₃ at 0^oC & 1 atm pressure, doesn’t have Avogadro’s number of molecules.

(c) Justify that 1 cm³ of H₂ and 1 cm³ of CH₄ at STP will have same number of molecules, when one molecule of CH₄ is 8 times heavier than that of hydrogen.

According to Avogadro’s law, equal volumes of all gases, under same conditions of temperature and pressure, contain equal number of molecules. So, 1 cm³ each of H₂ and CH₄ at STP also contains equal number of molecules, no matter what their masses are. This is due to the reason that the volumes of gases are affected by the number not by the nature of molecules because they are so far apart (about 300 times of their diameters) that there masses or sizes don’t disturb their positions.

Q.10(a): Dalton’s law of partial pressure is only obeys by those gases which don’t have attractive forces among their molecules. Explain it.

Dalton’s law of partial pressures is obeyed only by those gases whose molecules don’t attract each other. This is because if there were attractions among different gas molecules, the total pressure will become less than the sum of the individual partial pressures of the component gases, which is against Dalton’s law.

(b) Derive an equation to find out partial pressure of a gas knowing the individual moles of a component gases and the total pressure of the mixture.

Ans:

(c) Explain that the process of reparation obeys the Dalton’s law of partial pressures.

The process of respiration depends upon the difference in partial pressures of oxygen inside the lungs and in external air. When animals inhale, O₂ moves from air into their lungs and diffuses into blood, because the partial pressure of O₂ in air is 159 torr, while in lungs’ blood is 116 torr. During exhalation, CO₂ moves in opposite direction i.e., from blood in lungs into external air, as its partial pressure is more in the blood than in outer air.

(d) How do you differentiate between diffusion and effusion? Explain grahams law of diffusion.  

Q.11(a): What is critical temperature of a gas? What is its importance for liquefaction of gases? Discuss Lind’s method of liquefaction of gases.

Ans: A gas can be liquefied by applying pressure only when it is present at or below its critical temperature. Above its critical temperature, a gas can never be liquefied how much pressure may be applied. This is because, above this temperature, the gas molecules have so much high energy that intermolecular forces cannot bind them into liquid. So, critical temperature is an essential criterion to be considered for the liquefaction of gases.

(b) What is Joule-Thomson effect? Explain its importance in Linde’s method of liquefaction of gases.

Ans:

Joule-Thomson Effect: “When a highly compressed gas is allowed to expand into a region of low pressure, it gets cooled. This is called Joule-Thomson effect.”    

Explanation: In highly compressed state, the gas molecules are very close to each other, so appreciable attractive forces are present among them. When this gas is released into an area of low pressure, its molecules try to move apart. For this purpose, they require energy to overcome the intermolecular forces. For this purpose, the molecules utilize their own energy and, as a result, become cool.

Q.12(a) What is the kinetic molecular theory of gases? Give its postulates.

Kinetic Molecular Theory of Gases:

Bernoulli (1738) put forward molecular theory of gases to explain the behaviour of gases quantitatively. This theory provides a framework for understanding the macroscopic properties of gases such as pressure, volume and temperature, in terms of the microscopic behaviour of their constituent particles such as atoms or molecules.

Following are the fundamental postulates of this kinetic theory of gases.

1. Every gas consists of a large number of very small particles called molecules. Gases like He, Ne, Ar have monoatomic molecules.
2. The molecules of a gas move haphazardly, colliding among themselves and with the walls of the container and change their directions.
3. The pressure exerted by a gas is due to the collisions of its molecules with the walls of a container. The collisions among the molecules are perfectly elastic.
4. The molecules of a gas are widely separated from one another and there are sufficient empty spaces among them.
5. The molecules of a gas have no forces of attraction for each other.
6. The actual volume of molecules of a gas is negligible as compared to the volume of the gas.
7. The motion imparted to the molecules by gravity is negligible as compared to the effect of the continued collisions between them.
8. The average kinetic energy of the gas molecules varies directly as the absolute temperature of the gas.

(b) How does kinetic molecular theory of gases explain the following gas laws?

(i) Boyle’s Law

(ii) Charles’ Law

(iii) Avogadro’s law

(iv) Graham’s law of diffusion

Ans: Kinetic theory of gases gives birth to kinetic equation of gases, which can be employed to justify the
gas laws. In other words, it proves that gas laws get their explanation from kinetic theory of gases.

(i) Boyle’s Law:

(i) Charles’ Law:

(i) Avogadro’s Law:

(i) Graham’s Law of Diffusion:

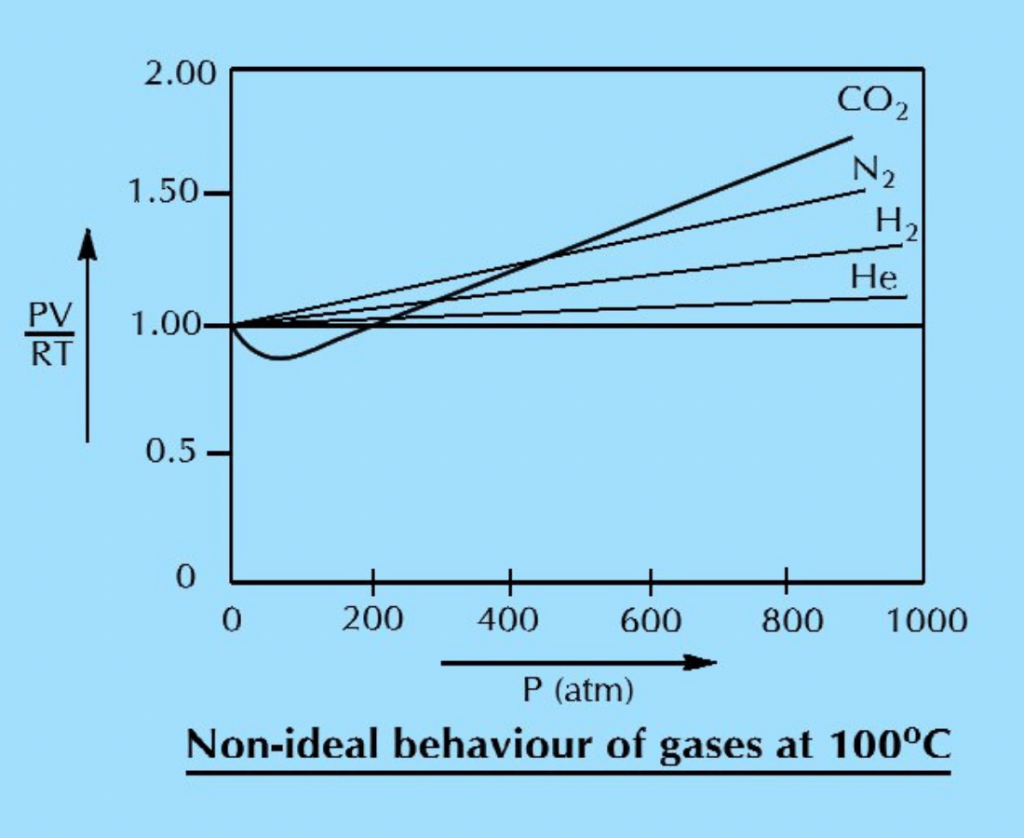
Q.13(a) Gases show non-ideal behavior a low temperature and high pressure. Explain this with the help of graph.

Ans: Gases show non-ideal behaviour at low temperature and high pressure. This can be explained by drawing a graph between pressure (P) on x-axis and compressibility factor PV/nRT on y-axis. The compressibility factor PV/nRT has a constant value equal to unity under all conditions for an ideal gas. This constant shows that the increase of pressure decreases the volume in such a way that PV/nRT remains constant at a constant temperature. So, a straight line is obtained parallel to the pressure axis, as shown in the figure. The real gases, however, show marked deviations from this behaviour. For example:

(b) Do you think some postulated of KMT are faulty? Point out these postulates.

Faulty Postulates of Kinetic Molecular Theory: The real gases deviate from ideal behaviour due to the two faulty postulates of kinetic molecular theory. These postulates are:

1. ‘There are no forces of attraction among the molecules of a gas.’ This is true at low pressure and high temperature when the molecules are far apart. But at high pressure and low temperature, the gas molecules are very close to each other and attractive forces operate among them. So, the gases deviate from ideality.
2. ‘The actual volume of the gas molecules is negligible as compared to the volume of the vessel.’ This is also somewhat true at low pressure and high temperature, but at high pressure and low temperature, when the gas molecules come close to each other, the actual volume of the gas molecules does not remain negligible. So, the gases deviate from ideality.

(c) Hydrogen and helium are ideal at room temperature, but SO₂ and Cl₂ are non-ideal. How will you explain this?

Ans: H₂ & He are small, non-polar gases. They have very weak London dispersion forces as intermolecular forces. So, they behave ideally at room temperature.

Cl₂ is also a non-polar gas, but due to its large size and high polarizability, strong London dispersion forces exist among its molecules. So, it behaves non-ideally at room temperature.

SO₂ is a polar gas, having large size and high polarizability. It has strong intermolecular forces (both dipole-dipole and London dispersion forces), so it also behaves non-ideally at room temperature.

Q.14(a): Derive van der Waal’s equation for real gases.

(b) What is the physical significance of van der Waal’s constants, “a” and “b”? Give their units.

Ans: (a) Consult the textbook article 3.10.2 for complete derivation of van der Waal’s real gas equation.

(b) Physical Significance of van der Waal’s Constants:

Van der Waals’ real gas equation is:

Here ‘a’ and ‘b’ are called van der Waal’s constants.

‘a’ is called co-efficient of attraction or attraction per unit volume. It is the measure of the attraction between the gas molecules. Greater value of a’ indicates greater attraction between gas molecules, and therefore greater deviation from ideality.

‘b’ is excluded or effective volume. It is the volume of one mole of a gas in highly compressed state but not in liquid state. Greater value of ‘b’ means greater space occupied by the gas molecules, less space is available for their motion, so greater deviation from ideality.

Q.15: Explain the following facts:

(i) The plot PV versus P is a straight line at constant temperature and with a fixed number of moles of an ideal gas.

(ii) The straight line in (a) is parallel to pressure axis and goes away from the pressure axis at higher temperatures for many gases.

(iii) Pressure of NH₃ gas at a given conditions (say 20 atm pressure and room temperature) is less as calculated by van der Waals equation than that calculated by general gas equation.

At 20 atm pressure and room temperature, strong hydrogen bonding exists between NH₃ molecules, due to which the pressure exerted by gas molecules on the walls of the container decreases. So, the real pressure of NH₃, calculated by van der Waals’ real gas equation ‘ ’ will be less than the ideal pressure of NH₃, calculated by ideal gas equation, PV=nRT.

(iv) Water vapors do not behave ideally at 273k.

Ans: Water vapours don’t behave ideally at 273 K because this is the freezing point of water. At such low temperature, water molecules in the vapour phase come very close to each other and strong hydrogen bonding operate among them. Thus, their real pressure becomes less than the ideal pressure, so they do not follow ideal gas equation or PV=nRT.

(v) SO₂ is comparatively non-ideal at 273K but behaves ideally at 373K.

Ans: SO₂ behaves non-ideally at 273 K because at such low temperature, the gas molecules come very close to each other and strong intermolecular forces start operating between them. So, the ideal gas equation PV=nRT is not obeyed. 

SO₂ behaves ideally at 373 K because at this temperature the gas molecules go far away from each other. The attractive forces between them become very weak, and the ideal gas equation, PV=nRT is followed.

Q.16: Helium gas in a 100 cm³ container at a pressure of 500 torr is transferred to a container with a volume of 250 cm³. What will be the new pressure?

a) If no change in temperature occurs.

b) If its temperature changes from 20°C to 15°C?

Ans:

Q.17: a) What are the densities in kg dm^–3 of the following gases at STP (P=101325 Nm^-2, T=273 K, molecular masses are in kg mol^–1)? (i) Methane (ii) Oxygen    (iii) Hydrogen   

b) Compare the values of densities in proportion to their molar masses.

From the above comparison, it is clear that the greater is the molar mass of a gas, the greater is its density and vice versa. It means density is directly proportional to the molar mass (d=PM/RT). The densities of these gases decrease in the following order: O₂ > CH₄ > H₂

c) How do you justify that increase of volume up to 100 dm³ at 27°C of 2 moles of NH₃ will allow the gas behave ideally, as compared to STP conditions?

Ans:

2 moles of NH₃ at 27^oC, having volume 100 dm³ will behave more ideally as compared to same amount of the gas at STP (0^oC & 44.8 dm³ volume). This is because gases become more ideal at higher temperatures, when their volumes increase and attractive forces become weaker.

Q.18: A sample of krypton with a volume of 6.25 dm³, a pressure of 765 torr and a temperature of 20°C is expanded to a volume of 9.55 dm³, and a pressure of 375 torr. What will be its final temperature in ^oC?

Q.19: Working at a vacuum line, a chemist isolated a gas in a weighing bulb with a volume of 255 cm³, at a temperature of 25°C and under a pressure in the blub of 10.0 torr. The gas weighed 12.1 mg. What is molecular mass of this gas?

Q.20: What pressure is exerted by a mixture of 2.00 g of H₂ and 8.00 g of N₂ at 273 K in a 10 dm³ vessel?

Q.21: (A) The relative densities of two gases A and B are 1 : 1.5. Find out the volume of B which will diffuse in the same time in which 150 dm³ of A will diffuse?

(B): Hydrogen (H₂) diffuses through a porous plate at a rate of 500 cm³ per minute at 0°C. What is the rate of diffusion of oxygen through the same porous plate at 0°C?

(C): The rate of effusion of an unknown gas A through a pinhole is found to be 0.279 times the rate of effusion of H₂ gas through the same pinhole. Calculate the molecular mass of the unknown gas at STP.

Q.22: Calculate the number of molecules and the number of atoms in the given amounts of each gas.

(a) 20 cm³ of CH₄ at 0°C and pressure of 700 mm of mercury

(b) 1 cm³ of NH₃ at 100°C and the pressure is decreased by 100 torr.

Q.23: Calculate the masses of 10²⁰ molecules of each of H₂, O₂ and CO₂ at STP. What will happen to the masses of these gases, when the temperature of these gases is increased by 100°C and the pressure is decreased by 100 torr.

Q.24(A): Two moles of NH₃ are enclosed in a 5 dm³ flask at 27°C. Calculate pressure exerted by the gas assuming that:

(i) It behaves like an ideal gas.

(ii) It behaves like a real gas.

     a = 4.17 atm dm⁶ mol^-2

     b = 0.0371 dm³ mol^-1

(B): Also Calculate the amount of pressure lessened due to forces attractions at these conditions of volume and temperature.

Solution:

Ideal Pressure= 9.852 atm

Real Pressure= 9.34 atm

Pressure lessened = 9.852 – 9.34 = 0.512 atm

(C): Do you expect the same decrease in the pressure of two moles of NH₃ having a volume of 40 dm³ and at temperature of 27°C.

Hope, you have found the exercise solution satisfying. Give your opinion about our work. Thanks!